Tercer Milenio
En colaboración con ITA
Matemáticas contigo
Las matemáticas de la línea del horizonte
¿Sabrían calcular a qué distancia se halla esa línea del horizonte, azul turquesa, que dibujan el cielo y el mar y que se ve allá lejos? Es el reto lanzado desde la cubierta de un barco a un grupito de turistas entre los que se encuentra... un matemático.

Un una mañana soleada de otoño, nos embarcamos en una travesía marina y matemática por los puertos de Santoña, Laredo y proximidades. Nos pareció un buen plan para hacer con los niños ese domingo por la mañana. Formábamos un grupo de dos parejas y tres niños. El barco zarpaba a las 12. Era un día soleado y una ligera brisa nos traía el olor salado del mar. Al estar sentados en cubierta, la sensación era muy agradable, a pesar de las molestas mascarillas. Nos permitían movernos por toda la nave, que con mis hijos Pablo, Laura y su amiga Adriana, añadía un punto extra de aventura y una vía de escape.
Al despojarnos de nuestras mochilas, el capitán nos dio la bienvenida por megafonía y nos explicó brevemente el recorrido. Salíamos del puerto de Santoña, llegaríamos a Laredo, donde podríamos bajar y volver a embarcar en el siguiente barco de la ruta. Después continuábamos hasta las proximidades del espectacular faro del Caballo. Desde este punto regresaríamos al punto inicial.
Tras estas palabras, y después de unos segundos, sonó por megafonía una melodía de presentación y una grabación que ya nos acompañaría el resto del viaje. La voz era agradable, el estilo de narrar ameno y los temas que trataba eran los esperados: situación geográfica; montes, ríos, marismas y playas locales, y por supuesto una breve exposición de la historia de ambas localidades. También nos recordó algunas cuestiones técnicas muy ligadas a la navegación (aérea y marítima), en particular las unidades de longitud (milla náutica) y de velocidad (nudos).
Millas, arcos y ángulos
Desde 1929 se decidió adoptar internacionalmente la milla náutica como unidad de medida de longitud en la navegación. Recordemos que los ángulos se miden en grados, minutos y segundos. Una circunferencia tiene 360 grados; 1 grado, 60 minutos; y 1 minuto, 60 segundos. La milla náutica es la distancia de arco del meridiano terrestre de un ángulo de un minuto. Se fijó este valor como 1.852 metros. Mediante una sencilla operación lo vamos a comprobar.
Lo primero es considerar la Tierra como una esfera perfecta de radio r= 6.367 km. No es una mala suposición ya que, en realidad, es bastante esférica, el radio en los polos es 6.357 kilómetros, mientras que en el ecuador es 6.378 km, solamente 21 kilómetros de diferencia, un poco más del 0,3% de su valor máximo. Por lo tanto para obtener la equivalencia en metros de un arco cuyo ángulo sea un minuto operamos así: 1 milla= 2П r/(360 x 60)=(2 x 3,1416 x 6.367)/(360 x 60) =1.852 metros, donde hemos dividido por 360 x 60 ya que, como hemos dicho, 360 son los grados de una circunferencia y 60 los minutos que tiene un grado.
El nudo es la velocidad necesaria para recorrer una milla náutica en una hora. Es una unidad muy práctica, ya que permite trasladarla directamente a las cartas de navegación: a una velocidad constante de 6 nudos durante una hora, la embarcación habría recorrido un arco de 6 minutos de grado en esa hora. También se utiliza en meteorología para medir la velocidad de los vientos. Su nombre proviene de los antiguos sistemas de medición de velocidad de los barcos en los que se arrojaba una cuerda atada a un tronco y con nudos a distancia constante. Para determinar la velocidad de la nave, se iba soltando cuerda y contando los nudos en un tiempo fijo.
En la entrada del puerto de Laredo, unos enormes cubos perfectos de hormigón parecían que se habían caído de una caja de construcciones infantiles. Al salir a navegar hacia el faro del Caballo, la grabación propuso a los obligados oyentes un problema de matemáticas. "¿Sabrían ustedes calcular a qué distancia se encuentra esa línea del horizonte turquesa infinito que ven a su derecha?".
La osadía del locutor por plantear semejante pregunta un domingo por la mañana en mitad del mar, me hizo sonreír. Pero había algo más, me creó expectación por saber cómo resolvería la situación haciendo uso únicamente de sus palabras. Por supuesto, salió airoso del trance.
Calculemos
El cálculo de esta distancia es un ejercicio bastante sencillo de resolución de triángulos rectángulos, y por tanto del archiconocido teorema de Pitágoras. Hay que señalar que se realizan varias simplificaciones, la primera de ellas, es considerar la Tierra como una esfera perfecta de radio r= 6.367 km, ya comentada.
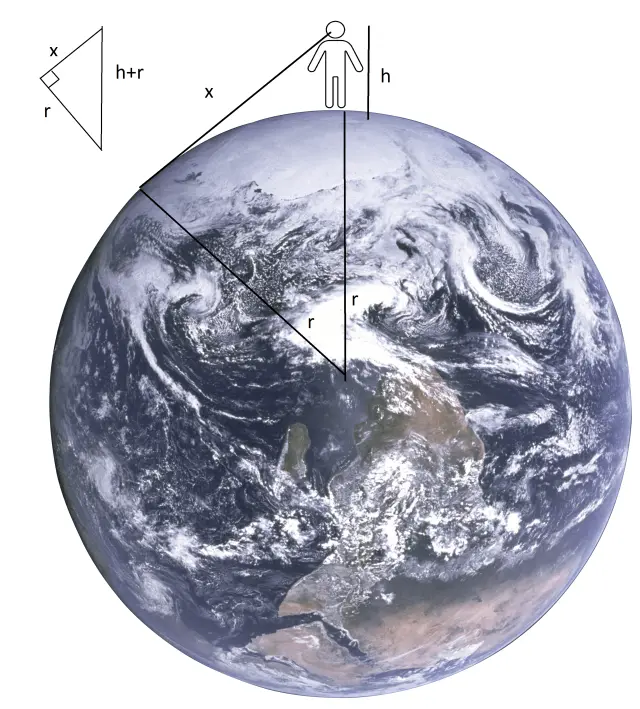
Es notable destacar que la distancia a la línea del horizonte, que llamaremos x, depende de la altura a la que se encuentra el observador. Supongamos que los ojos de nuestro observador están a una altura h. La visual desde el observador hasta la línea del horizonte es una recta tangente con la Tierra y, por lo tanto, forma un ángulo recto con el radio de la Tierra en ese punto. Si añadimos un tercer lado, desde el centro de la Tierra hasta los ojos del observador, habremos construido un triángulo rectángulo. Los dos catetos están formados por la incógnita x y el radio de la Tierra r, mientras que la hipotenusa medirá h+r. Por el teorema de Pitágoras, tenemos la igualdad x²+r²=(h+r)², y podemos despejar x en función de los datos r y h. Así, si tomamos por r= 6.367.000 m y x=1,5 m, obtenemos el valor aproximado de x= 4.370,46 m, esto es, casi 4,4 km.
El faro del Caballo, al que nos dirigíamos, se encuentra a una altura de 24 metros, y por lo tanto la línea del horizonte se sitúa a 17.482 m, aproximadamente 17,5 km. Ante estos números, uno entiende la ventaja que suponía situar a los vigías en la parte más alta de los mástiles de los barcos.
En los libros de náutica suele aparecer una aproximación de la fórmula anterior despreciando el valor de h² y obteniendo que x² es aproximadamente 2hr, ya que x²=(h+r)² - r²=h²+2hr. Si el lector aplica la aproximación 𝑥=√2hr en los ejemplos anteriores, obtendrá prácticamente los mismos valores de la distancia a la línea del horizonte. La grabación terminó diciendo que esa línea del horizonte marca la distancia en que los barcos de pesca de bajura salen a faenar, trayendo sardinas, jureles, alguna merluza o lubina.
El sol brillaba en lo más alto cuando llegamos al faro del Caballo. Desde el acantilado más alto y cortante, algunos valientes se lanzaban al agua. Más de 700 escalones hay que bajar (y subir) para llegar a pie a esta maravilla de lugar. Después de tomar las obligadas fotos, regresamos al punto de salida. Al desembarcar, dieron a los niños un certificado de marineros expertos, y marchamos todos satisfechos. Camino del restaurante, pensaba que ya tenía material para el siguiente artículo.
Pedro J. Miana Departamento de Matemáticas, Instituto Universitario de Matemática Aplicada y Facultad de Ciencias, Universidad de Zaragoza
-Ir al suplemento Tercer Milenio
Apúntate y recibe cada semana en tu correo la newsletter de ciencia



