Ha afectado a muchos de los más insignes topólogos de los dos últimos siglos, comenzando por el propio Henri Poincaré, el padre de la criatura -perdón, de la conjetura (buen momento para aclarar que una conjetura es una afirmación sin pruebas; una vez que ha sido demostrada se convierte en teorema)-, de quien la enfermedad toma su nombre y quien asimismo nos brindó una elegante definición de qué es la Topología: “lo que queda de la Geometría cuando se prescinde de las distancias”. 

En efecto, la Topología, una de las ramas más recientes de las Matemáticas, surgida en el siglo XVIII y que recibió su primer gran impulso a caballo entre el siglo XIX y XX de la mano de Poincaré, se dedica al estudio de la esencia de los objetos espaciales, léase cuadrados, esferas, nudos, pero también el cosmos, el espacio-tiempo o cualquier otro objeto de n-dimensiones. Y con eso de la “esencia”, lo que se quiere indicar es que los topólogos no se preguntan por la longitud, la altura o el ángulo de dichos objetos espaciales, sino sobre si tienen huecos (o vacíos) o por el contrario son continuos, el número de intersecciones que presentan, si todas las partes están interconectadas entre sí o hay regiones “separadas” y, sobre todo, si el objeto espacial en cuestión se puede deformar hasta convertirse en otro. 

Porque ahí radica el quid de la Topología: dos objetos espaciales son equivalentes (homeomorfos) cuando uno se puede transformar en el otro a base de deformarlo; comprimiéndolo, estirándolo o retorciéndolo, pero nunca rompiéndolo o cortándolo. 

Te puede interesar

Miguel Barral: "Un peculiar humor impregna lo que escribo"

TERCER MILENIO: 30 ANIVERSARIO

De este modo, para los topólogos, un círculo y un cuadrado son exactamente lo mismo al tiempo que nunca podrían ser confundidos -convertidos- en una cruz. la geometría de la goma elástica Si se clavan cuatro chinchetas en un corcho y se coloca alrededor de ellas una goma elástica se obtiene un paralelogramo. Si entonces retiramos una de las chinchetas lo habremos convertido, “deformándolo”, en un triángulo. Si se suelta otra chincheta más, lo que se tiene es una elipse muy excéntrica. Y si se retira una tercera chincheta, la goma adoptará la forma circular. Por lo tanto, desde el punto de vista topológico un paralelogramo, un triángulo, una elipse y un círculo son equivalentes, ya que todos ellos consisten en una banda cerrada o continua. Algo que no se puede decir de una cruz ya que, se ponga uno como se ponga y ponga las chinchetas donde las ponga, nunca podrá convertir la goma en una. El que no lo vea, que no se “corte” y haga la prueba.

Por todo lo anterior, a la Topología también se la denomina como la Geometría de la lámina de goma o de la superficie elástica. Y de ahí también el famoso chascarrillo matemático que presenta a los topólogos como aquellos matemáticos incapaces de distinguir un donuts de una taza de café. No le falta razón por cuanto ambos son objetos espaciales cuya naturaleza esencial es la de poseer un hueco. Si uno piensa en una taza de café fabricada en un material deformable no es difícil imaginar cómo se podría convertir en una rosquilla.

De boca a boca

Es posible que la Topología parezca una disciplina desconectada de la realidad. Nada más lejos de aquélla. De un modo intuitivo todos aplicamos el razonamiento topológico a diario. Cada vez que planificamos un itinerario, ya sea sobre un mapa o mentalmente, la Topología lleva la voz cantante. En ese momento no pensamos en distancias, pendientes de las cuestas o si la carretera es recta o tiene una curva más o menos cerrada, sino en cruces, conexiones y atajos. En otras palabras, en el aspecto cualitativo del trayecto, en su esencia. Algo que podemos visualizar con la ayuda de un plano de las líneas del metro, que no es ni más ni menos que un plano topológico. No aporta información sobre la distancia que separa cada parada entre sí, ni sobre si el trayecto es recto o curvo, cuesta arriba o cuesta abajo. Lo único que indica es si la línea es un circuito cerrado o abierto, cómo se conectan las distintas líneas entre sí y si se puede pasar de una a otra. Suficiente para saber cómo ir de boca (de metro) a boca. 

¿El último afectado?

La poincaritis experimentó un rebrote en el año 2000 a raíz de que el Instituto Clay para las Matemáticas incluyese la conjetura entre sus siete problemas del milenio y en consecuencia ofreciese un premio de un millón de dólares a quien la resolviese. No obstante, no fue ésta la vía por la que contrajo la enfermedad el matemático ruso Grigory Perelman, desa-parecido del circuito matemático desde 1994 y que ocho años después, en 2002, reapareció con un increíble anuncio: había conseguido demostrar la conjetura de poincaré, el reto al que había consagrado todos ese tiempo. Sin embargo, a la hora de enseñar su demostración, Perelman se saltó los cauces convencionales. En lugar de presentar un artículo a una prestigiosa revista matemática para su publicación, optó por colgar, entre noviembre de 2002 y julio de 2003, sus trabajos en Internet. 

Dado el hermetismo del matemático ruso, sólo cabe conjeturar que esta decisión estuviese motivada por la aparición en 2002, justo antes de que Perelman hiciese su anuncio, de un artículo de los matemáticos japoneses Shioya y Yamaguchi en el que demostraban una serie de resultados que Perelman ya habría obtenido con anterioridad durante el proceso de demostración de la conjetura. Es probable que el temor a que alguien le pudiese robar la gloria fuese el factor decisivo que le impulsó a tomar la decisión de difundir su trabajo por Internet, donde su publicación sería inmediata al no tener que superar una revisión previa por parte de los evaluadores de la revista. Pero, paradójicamente, al recurrir a esta vía Perelman se arriesgó a perder la recompensa puesto que las normas del premio exigen la publicación de trabajo en una revista matemática de prestigio. Por fortuna para el ruso, los responsables del Instituto Clay anunciaron que le concederían igualmente el premio siempre que la demostración superase el periodo de dos años expuesta al análisis de la comunidad matemática a partir de su publicación y establecido asimismo en las bases del premio. 

Un trabajo de chinos

En 2006, transcurridos casi tres años, existe un convencimiento general entre los matemáticos de que la solución de Perelman es “la buena” y lo único que falta para confirmarla es que se acaben de comprobar algunos detalles “técnicos” englobados en la parte más compleja del desarrollo. Pero lo más importante es que, con lo que ya se ha aceptado hasta ahora, la conjetura de Poincaré queda demostrada.

Por este motivo, existe una gran expectación y también cierto convencimiento de que el Congreso Matemático Internacional 2006, que se celebrará del 22 al 30 de agosto en Madrid, puede ser el momento escogido para hacer oficial la demostración aprovechando que la conjetura de Poincaré será uno de los temas centrales del encuentro y que en él participarán dos de los principales expertos en la cuestión -no así Perelman, que ha rechazado la invitación-.

Es en este escenario en el que el pasado 10 de mayo se anunció que dos matemáticos chinos, Zhu Xiping y Cao Huaidong, han dado con la solución de la conjetura de Poincaré. Solución que, dicho sea de paso y como han reconocido sus propios autores, está basada en la descripción de Perelman sobre cómo demostrar la conjetura y que los matemáticos chinos afirman haber llevado hasta el final.

Y es asimismo este escenario el que permite entender por qué este anuncio ha tenido mucha más repercusión entre los medios de información general -periódicos, telediarios, etc.- que en los especializados y entre la comunidad matemática. Lógico, ya que para sus miembros, la demostración ya existe y sólo están a la espera de que se anuncie de forma definitiva el descubrimiento de la vacuna contra la poincaritis.

Estoy hecho un nudo

Aunque la esencia de la Topología sea estudiar y clasificar los distintos objetos espaciales, tiene también numerosas aplicaciones. Una de las principales es la abstracción de la conectividad inherente de los objetos ignorando su forma. Que dicho así suena francamente mal pero que no consiste en otra cosa que procesar sistemas de lo más diverso, de la misma manera que se ha hecho con las líneas de metro: reduciendo los elementos que integran el sistema a puntos y observando cómo éstos están conectados entre sí. 

A esta rama de la Topología se la conoce como Teoría de grafos y se aplica, entre otras cosas, para optimizar el diseño de circuitos eléctricos, redes de comunicación, organigramas de empresas, redes informáticas, etc. La otra rama de la Topología que en la actualidad se muestra especialmente activa es la Teoría de nudos, que se encarga de estudiar las propiedades de éstos y de clasificarlos en consecuencia, y que ha encontrado sorprendentes campos de aplicación tanto en la Física cuántica, en el estudio de las partículas fundamentales vistas como estructuras superenrolladas; como en la Biología molecular, facilitando la comprensión y estudio de las estructuras de macromoléculas como el ADN. La actividad y propiedades del material genético vienen determinadas por el tipo de deformaciones y anudamientos que presenta. En este sentido, la Topología permite identificar cada porción del ADN con un tipo de nudo concreto y conocer así sus características.

Monsieur Poincaré tiene la palabra

En 1904, Henri Poincaré se planteó la siguiente cuestión (en éstos o parecidos términos): si un espacio cerrado de dimensión tres tiene la propiedad de que toda curva cerrada se puede deformar a un punto ¿es topológicamente una esfera? Expresada en un lenguaje comprensible por todos, lo que plantea es que la esfera tridimensional es el único espacio cerrado de tres dimensiones que no contiene agujeros. Y como era de temer, una esfera tridimensional no es nuestra familiar esfera, que es bidimensional, sino su equivalente con una dimensión adicional. Es decir, el conjunto de puntos situados a la misma distancia del origen en un espacio de cuatro dimensiones. Eso sí, la esfera bidimensional, la de toda la vida, es igualmente el único espacio cerrado sin agujeros que existe en un espacio tridimensional, algo que se sabe desde el siglo XIX.

Poincaré estaba convencido de que la respuesta era afirmativa. No en vano, cuatro años antes había elaborado una demostración para la que, sin embargo encontró un contraejemplo que la frustraba. Tras su formulación pública, otros matemáticos, además de convencerse de la validez de la conjetura, también intentaron alcanzar una demostración, algo que propició un conocimiento más profundo de los espacios topológicos, que desembocó en una generalización del problema para esferas y espacios de cualquier dimensión, dando lugar a una versión del problema conocida como la Generalización de la conjetura de Poincaré y que, por sorprendente que resulte, fue demostrada sucesivamente para todas las dimensiones excepto para el caso original, el del espacio tetradimensional… ¿Hasta ahora?

La topología es un juego de niños

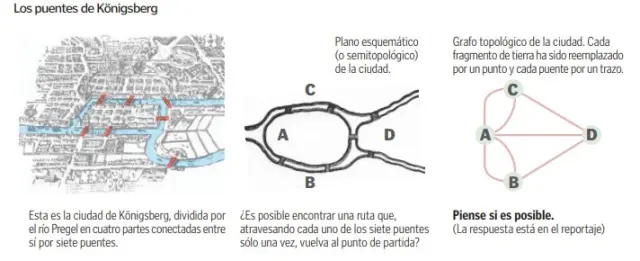
Algunos de los más famosos problemas topológicos son mucho más intuitivos y fáciles de digerir que la conjetura de Poincaré, hasta el punto de que, en ocasiones, son enunciados como pasatiempos matemáticos. El mejor ejemplo es el célebre problema de los puentes de Königsberg, surgido sobre 1700 y que plantea si es posible recorrer esta ciudad rusa dividida en cuatro partes por el río Pregel, pasando una vez y sólo una sobre los siete puentes que cruzan el río y conectan las distintas zonas entre sí. Leonhard Euler fue el encargado de resolver el problema en 1736, para lo cual recurrió a convertir cada parte de la ciudad en un punto y los puentes en trazos que conectaban los distintos puntos. La solución de Euler marca el nacimiento de la Teoría de grafos.

Otro problema topológico de tintes recreativos es el del mapa de los cuatro colores, enunciado en 1852 y que plantea que para colorear cualquier mapa “topolítico” de modo que dos regiones que comparten frontera tengan siempre distinto color sólo se necesitan cuatro colores. Bajo este lúdico enunciado se esconde una conjetura que durante más de un siglo desafió a los matemáticos y que, en 1996, pudo ser confirmada -y elevada a teorema- mediante la aplicación de la Teoría de grafos.