Tercer Milenio
En colaboración con ITA
Matemáticas contigo
Las telas de araña matemáticas de Spiderman
Cuando menos te lo esperas, las matemáticas aparecen para mostrarnos que hasta un superhéroe como Spiderman necesita conocerlas para derrotar a sus enemigos.

La celebración del noveno cumpleaños de Aimar, uno de los mejores amigos de mi hijo Pablo, fue invitar a los cuatro miembros de ‘la Pandilla’ al cine. Llevaban varias semanas, y creo que incluso algún mes, hablando ilusionados de la película ‘Spiderman: No way home’. Era la tercera entrega protagonizada por Tom Holland y Zendaya dentro del universo Marvel. Aunque mi héroe favorito Marvel siempre ha sido Ironman, para los cuatro amigos este jovencísimo y divertido Spiderman se había convertido en su héroe particular.
Por supuesto, les cogimos los cuatro asientos juntos y separados de los padres. Antes, les cargamos de palomitas (compradas fuera del cine), agua y bastantes chuches, permitidas en este día tan especial. En la fila de atrás, los padres nos sentamos confiando que las buenas críticas recibidas por la película fueran justificadas y pudiéramos compartir esa ilusión de volver ir al cine, sentirnos niños y quedar atrapados en la historia contada en la pantalla.
La trama de la película iba evolucionando, acompañada de diálogos afilados y de las esperadas escenas de acción. El enfrentamiento previsible entre el Dr. Strange y Spiderman se resuelve a favor del segundo cuando este se da cuenta de que la ilusión creada por el primero en la dimensión espejo viene modelizada por la espiral de Arquímedes. Después de unos cálculos, algunos de ellos sin sentido, el hombre-araña identifica la posición exacta del mago y, antes de inmovilizarlo con su tela de araña, le espeta al Dr. Strange:
–Lo que mola más que la magia son las matemáticas.
Como matemático, esta frase me hizo incorporarme en el asiento y sonreír. El aprecio por las matemáticas había llegado a las superproducciones de Hollywood. Saioa, madre de Aimar, me dio un codazo, mientras que Claire, física de formación y matemática de vocación también, sonrió mientras abría aún más sus ojos verdosos.
El genio griego Arquímedes estudió esta fascinante curva en el tratado ‘Sobre espirales’ escrito alrededor de 225 A. C. Además, la empleó para resolver problemas clásicos de las matemáticas griegas, como la trisección de un ángulo o la cuadratura del círculo. También probó que el área limitada por la primera espiral es 1/3 del área del círculo de radio la amplitud final de la espiral.
Claire se acercó y, apartando su hermosa melena pelirroja a un lado, me comentó:
–Sabía que las primeras grabaciones para gramófonos se realizaron en surcos que describían espirales de Arquímedes; y que también para diagnosticar enfermedades neurológicas, se pide a los pacientes que tracen espirales de Arquímedes. Pero nunca había imaginado que Spiderman las pudiera utilizar para vencer a sus enemigos.
Entregados ya a la película, la trama se centró en la posibilidad de universos paralelos, lo que se denomina ‘multiverso’. Aunque es una teoría con siglos de historia, el termino ‘multiverso’ fue acuñado por el filósofo estadounidense William James en 1895. Plantea la posibilidad de que el universo tuviera varias o incluso infinitas copias y que las cosas ocurrieran de forma diferente en cada realidad. Incluso podría existir un multiverso matemático, denominado ‘omniverso’, en el que todo universo que pudiera ser descrito matemáticamente existiera. Esta última teoría fue propuesta por el físico teórico, y antes niño prodigio de las matemáticas, Brian R. Greene.
En el universo Spiderman, también existen universos paralelos, concretamente tres. Las comunicaciones entre los diferentes universos se producen a través de portales que abre el portador de un anillo mágico y que consigue reunir a los tres últimos protagonistas que se han enfundado el traje.
Avanzando hacia al final, era difícil decidir si les estaba gustando más a los niños –Pablo saltaba en su asiento– o a los entregados padres y madres –a Claire le brillaban los ojos–. Y aún restaba una pequeña sorpresa. La canción ‘3, The Magic Number’ del grupo De La Soul e incluida en el disco ‘Smell the D.A.I.S.Y’ (2014) acompaña a unos créditos maravillosos con contenido matemático y cuidado diseño.
Al encender la luz, regresamos a nuestro universo. Recogimos nuestras cosas, comentamos escenas y, con algún pequeño haciendo de Spiderman por las paredes, salimos de la sala. Con el objetivo cumplido de calar ilusión, nos encaminamos al parque.
La espiral de Arquímedes
La famosa espiral de Arquímedes es el sustituto natural de la línea recta cuando cambiamos los sistemas de coordenadas en un espacio bidimensional. Las coordenadas cartesianas (abscisas y ordenadas) miden la distancia de un punto a los ejes coordenados, de ordenadas y de abscisas respectivamente. Las líneas rectas tienen por ecuación y= ax +b y son los lugares geométricos del plano más sencillos, determinan las ordenadas (variable y) en función de las abscisas (variable x) y de las constantes a y b que definen la recta. El sistema cartesiano, nombre en honor a su inventor el matemático y filósofo francés René Descartes (1596-1650), no es el único sistema de referencia del plano. Podemos elegir como sistema de referencia la distancia de un punto al origen de coordenadas (también llamado polo) y el ángulo que forma el vector de posición del punto y el eje de las abscisas positivas. Ambas variables se representan por (r, θ) y se les llama coordenadas polares.
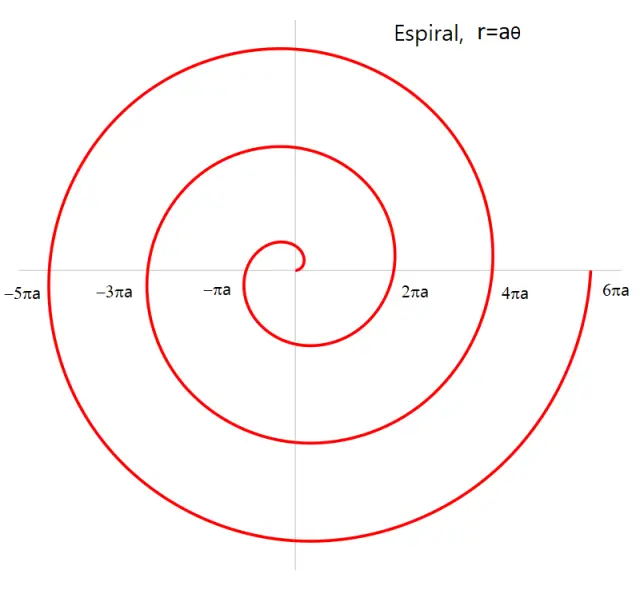
Los ángulos en matemáticas se miden en radianes. Los radianes tienen una gran ventaja sobre los grados (°), minutos (’) y segundos (”) (otras unidades que miden ángulos). La longitud del arco de una circunferencia de radio r y ángulo θ (en radianes) es exactamente rθ. Así el ángulo de 90º tiene exactamente π/2 radianes; el de 180º son π radianes y la circunferencia completa 2π radianes. Un radián son aproximadamente 57° 17’ 44,8”.
Si ahora consideramos la ecuación r= aθ +b, donde (r, θ) con las coordenadas polares y los parámetros a y b constantes, obtenemos una bonita espiral de Arquímedes, donde b marca el origen de espiral y el parámetro a la anchura de la espiral, constante en cada vuelta.
Pedro J. Miana Departamento de Matemáticas, Instituto Universitario de Matemáticas y Aplicaciones (IUMA) & Facultad de Ciencias, Universidad de Zaragoza
-Ir al suplemento Tercer Milenio
Apúntate y recibe cada semana en tu correo la newsletter de Tercer Milenio



