Tercer Milenio
En colaboración con ITA
Ciencia en casa
El poder de la potencia, de recompensas a contagios
De la recompensa que pidió el inventor del ajedrez al ritmo de contagio de la covid-19.

- Voy, pues, a aceptar por el juego que inventé, una recompensa que corresponda a vuestra generosidad; no deseo, sin embargo, ni oro, ni tierras, ni palacios. Deseo mi recompensa en granos de trigo.
- ¿Granos de trigo? –exclamó el Rey, sin ocultar la sorpresa que le causara semejante propuesta. ¿Cómo podré pagarle con tan insignificante moneda?
- Nada más simple –aclaró Sessa-. Dadme un grano de trigo por la primera casilla del tablero, dos por la segunda, cuatro por la tercera, ocho por la cuarta y así duplicando sucesivamente hasta la sexagésima cuarta y última casilla del tablero. Ruego a vos, rey generoso, que de acuerdo con vuestra magnífica oferta, ordenéis el pago en granos de trigo, y así como te indiqué.
- ¡Qué tonto! –exclamó mi hijo Pablo, interrumpiendo la lectura del Capítulo XVI del maravilloso libro 'El hombre que calculaba' de Malba Tahan. Podía escoger oro o diamantes y solo ha pedido trigo. ¿Para qué lo quiere; va a hacer barras de pan?
- Ya, pero no se sabe cuánto quiere – le respondí. Para saberlo hay que calcularlo. Si te parece, podemos intentarlo con el tablero de nuestro ajedrez y con granos de arroz, ya que trigo no tenemos. Vamos a ello.
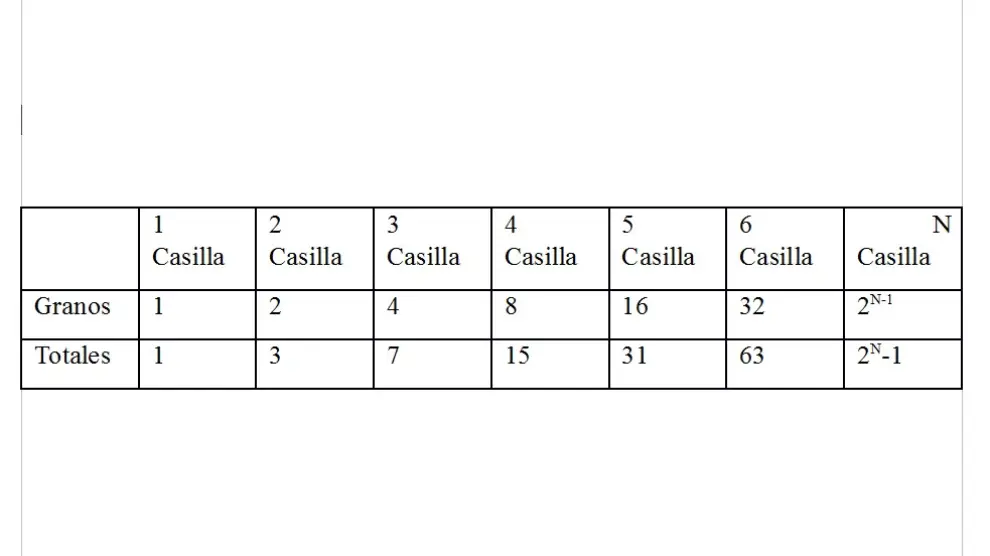
Como hay 64 casillas solo hay que calcular cuánto es 2⁶⁴-1, y esto es, 2⁶⁴-1 = 18.446.744.073.709.551.616 granos de trigo.
-¿Y eso es mucho trigo?, se preguntó Pablo y yo también, la verdad. Aproximadamente 25.000 granos de trigo hacen un kilo. Por tanto necesitamos 18.446.744.073.709.551.616:25.000 = 737.869.762.948.382 kg de trigo.
Se estima que la producción mundial de trigo en el año 2019 se situó alrededor de 730 millones de toneladas. Por tanto, hagamos una última división, 737.869.762.948.382:730.000.000.000 = 1.010,7804971895643836 años.
- Así que necesitamos más de 1.000 años para recompensar al inventor del ajedrez. Pablo, ya ves, - le dije- eligió un gran recompensa, y una lección nueva nos ha dado, la potencia de un número puede crecer muy deprisa.
- Pero eso pasó hace mucho tiempo, papá, seguro que la potencia esa, ya ni se usa.
-La usamos cada día y más ahora. Te pongo otro ejemplo muy actual. Vinimos algo asustados por ese pequeño bichito, llamado coronavirus. Una de su característica más preocupante es su elevada velocidad de propagación. La Organización Mundial de la Salud sitúa la tasa de contagio (R0) entre 1,4 y 2, 5. ¿En cuántos días contagiará a toda España?¿ y a toda la humanidad?.
Para facilitar las cuentas y simplificar algo el problema (también por algo de vagancia), supongamos que un enfermo contagia al día a dos personas sanas, esto es, el número R0 es 2. La evolución de la pandemia en los primeros días también viene establecida por la misma tabla anterior. Así los contagiados en un día se duplican al día siguiente. De nuevo, el problema radica en lo rápido que crecen las potencias de dos.
A fecha 1 de enero de 2020, el Instituto Nacional de Estadística afirmaba que en España residían 47.431.256 de personas. En tan solo 26 días tendremos contagiadas a mucho más que toda España, a más de 67 millones, exactamente: 2²⁶-1=67.108.863.
Pero esto no se detiene aquí. Una semana más tarde, a los 33 días, se habría contagiado toda la población del planeta. Así, la población mundial según el último informe demográfico de las Naciones Unidas (2019) son 7.700 millones de personas y notemos que 2³³-1= 8.589.934.591.
La cara de Pablo se había transformado por la sorpresa y el miedo y me preguntó ¿Y qué podemos hacer?
- Para controlar la epidemia hay que rebajar la trasmisión, o bien obligando a quedarse en casa (confinamiento) o manteniendo la distancia de seguridad o ahora llevando la mascarilla. Matemáticamente si el número R0 está por debajo de 1, el número de casos disminuye y la epidemia se vence.
- Pues yo prefiero quedarme en casa, jugando al ajedrez contigo –dijo mientras quitaba el arroz y empezaba a colocar las piezas
Pedro J. Miana Departamento de Matemáticas. Instituto Universitario de investigación en Matemáticas y Aplicaciones. Universidad de Zaragoza
-Ir al suplemento Tercer Milenio


