Una pizza, un balón, una lata de refresco, la telefonía móvil… tienen algo en común, pi.

En cualquier objeto o recinto circular, al dividir su perímetro entre su diámetro se obtiene el mismo valor: 3,141592… al que llamamos π. Así que la longitud de la circunferencia es iguala a 2·π·r, siendo r el radio, y de ahí se deduce que el área del círculo es π·r². Da igual si se trata de una moneda, un neumático o una rotonda. π es una constante asociada a la forma circular, sea cual sea el tamaño de esta.

Al girar una figura plana 360º en torno a un eje se genera un cuerpo de revolución. Los más usuales son cono, cilindro y esfera. En las fórmulas de las áreas y volúmenes de todos ellos también aparece π. Hay muchas formas circulares y cuerpos de revolución a nuestro alrededor. Están en los productos de consumo, en la arquitectura, en el arte, en el deporte, etc. Al abordar las variadas cuestiones que sobre ellos haya que resolver, habrá que usar π.

Desde la antigüedad mesopotámica la unidad de medida de ángulos fue el grado. En 1874, Thomas Muir propuso otra unidad mayor, el radián, un ángulo cuyo arco en la circunferencia es igual al radio de esta. Los 360º equivalen a 2·π radianes y los ángulos más usuales, divisores de 360º, se expresan en radianes como fracciones de π (90º = π/2 radianes, 45º = π/4 radianes, etc.). La trigonometría, que permite medir lo inaccesible en muchos contextos (astronomía, navegación, topografía o arquitectura, entre otros), usa las propiedades de los triángulos y de sus ángulos. También ahí encontramos a π.

Los fenómenos naturales periódicos u oscilantes, como las ondas, se aproximan con sumas de funciones trigonométricas sencillas, las llamadas series de Fourier. Se usan en comunicaciones, para el proceso digital de señales; en el diagnóstico médico a partir de las vibraciones de la membrana del corazón; en los sintetizadores de música, etc. En esas series interviene π.

Y aún hay más apariciones de este número singular: en las elipses, en las espirales, en las curvas cardioide y astroide o incluso en las probabilidades. Por todo lo anterior, π es un compañero habitual en el estudio matemático de los problemas.

Una historia interminable que va por los 22,5 billones de dígitos

Aunque a efectos prácticos nos baste aproximar π con los valores 3,14 ó 3,1416, al ser un número irracional, su parte decimal tiene infinitas cifras que no siguen un periodo de repetición. Además, se supone que tampoco siguen pauta alguna. Así, conocer dichas cifras es una tarea inacabable. .

La historia comenzó en Babilonia (1900 a.C.), con la primera aproximación: 3,125. En el papiro de Rhind, escrito por el egipcio Ahmes (1.700 a.C.) se da el valor 3,16. Dice la Biblia (Libro Primero de los Reyes 7:23) que Hiram de Tiro (siglo X a.C.) mandó construir en el templo de Jerusalén una pileta circular de 30 codos de perímetro y 10 codos de diámetro. Según eso, π = 3… Un error bíblico.

Arquímedes (287-212 a.C.) tomó una circunferencia de diámetro unidad e hizo aproximaciones para saber su longitud que, en ese caso, es justamente π. Su método, llamado exhaustivo, consistía en calcular los perímetros de sucesivos polígonos regulares de 6, 12, 24, 48 y 96 lados, inscritos (la circunferencia pasa por su vértices) y circunscritos (los lados son tangentes a la circunferencia).

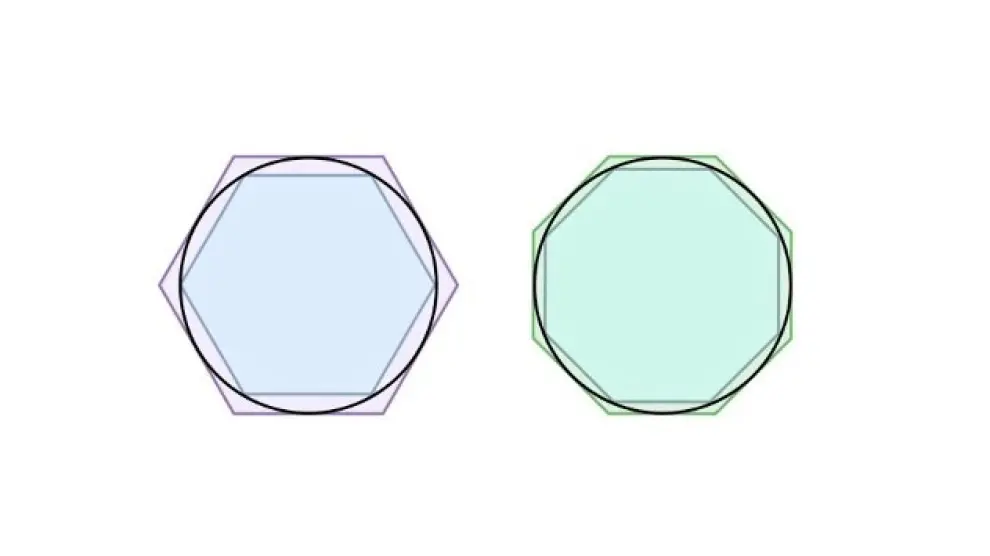
Esos perímetros cada vez están más próximos a la circunferencia y a partir de los 12 lados, en el dibujo son casi indistinguibles. Pero Arquímedes no necesitaba dibujarlos, le bastaba con calcular sus longitudes y esto puede hacerse, por ejemplo, aplicando repetidamente el teorema de Pitágoras. Así llegó a estas aproximaciones:

223/71 < π < 22/7 (número arquimediano)

En forma decimal: 3,14084< π <3,14286.

Claudio Ptolomeo (siglo II) utilizó el mismo método con polígonos de 720 lados y obtuvo el valor 3,14166. El chino Zhu Chongzhi (siglo V) llegó a la aproximación 3,1415926, que no fue mejorada hasta 1424 por el persa Al-Kashi. Este planteó un curioso problema: "Expresar la longitud de la circunferencia con tal precisión que su error, cuando el radio es igual a 600.000 diámetros de la Tierra, no supere el grosor de un cabello". Su solución consiguió 19 cifras decimales de π, para lo cual consideró polígonos de 3 por 2 elevado a 28  lados. Hubo que esperar al siglo XVII para que Adrian van Roomen llegase una cifra más lejos.

Ludolph van Ceulen (1540-1610) dedicó media vida a la tarea de aproximar π y llegó a obtener 35 decimales, mediante polígonos de 2 elevado a 62 lados. Orgulloso de ello, quiso que tal número, llamado en su honor ‘número ludolphino’, figurase en su tumba.

En 1647 William Ougthred dio a este número el nombre de π, primera letra de la palabra griega ‘periferia’. Su uso por el gran Leonhard Euler le dio universalidad. En esa época se pasó del método exhaustivo a las aproximaciones mediante series infinitas, llegando a 100 dígitos en 1706 (W. Jones) y a 527 dígitos en 1853 (W. Shanks).

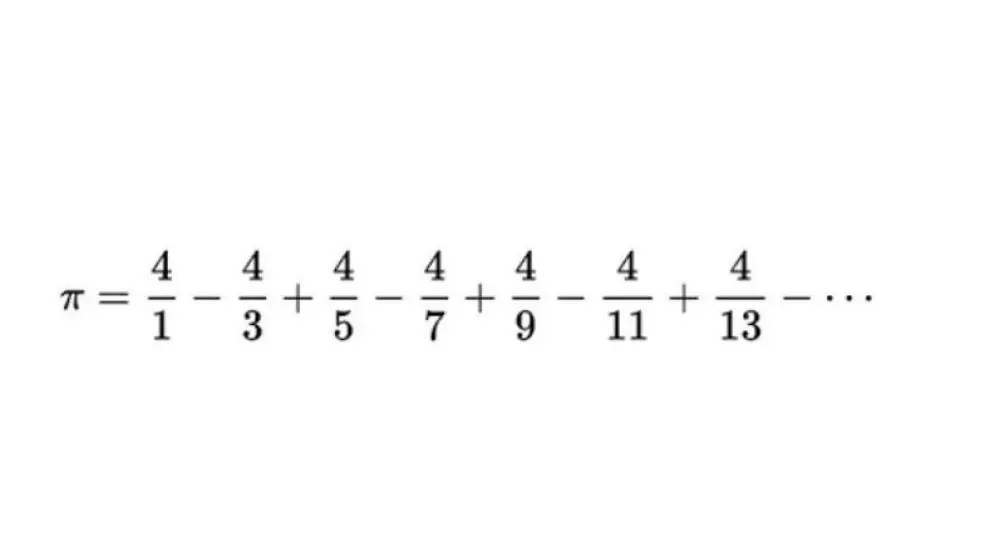
Muchos matemáticos buscaron series que converjan a π. Es célebre la que obtuvieron por separado Somayaji (1500) y Leibnitz (1673):

También, la de Wallis (1696):

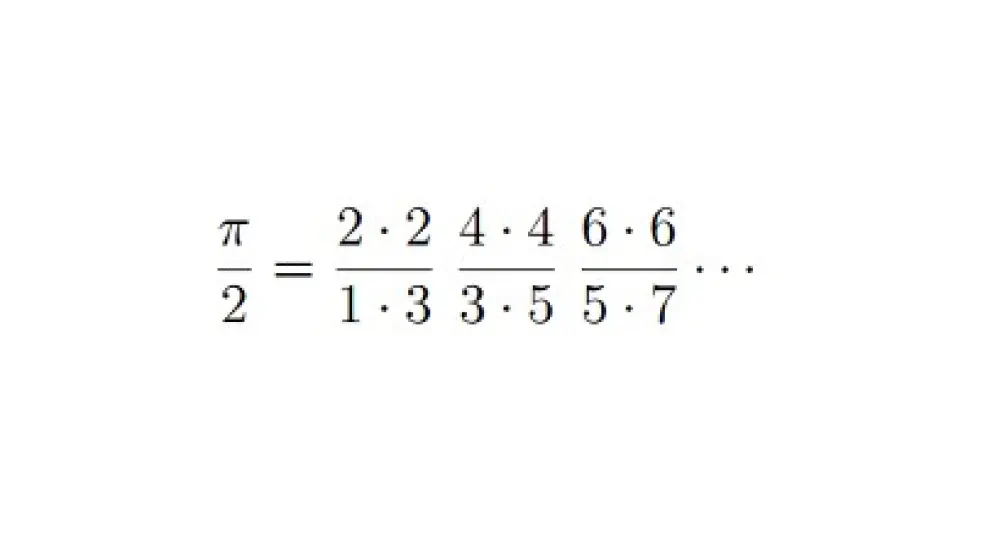
En el siglo XX, el indio Srinivasa Ramanujan sorprendió con series tan impresionantes como esta:

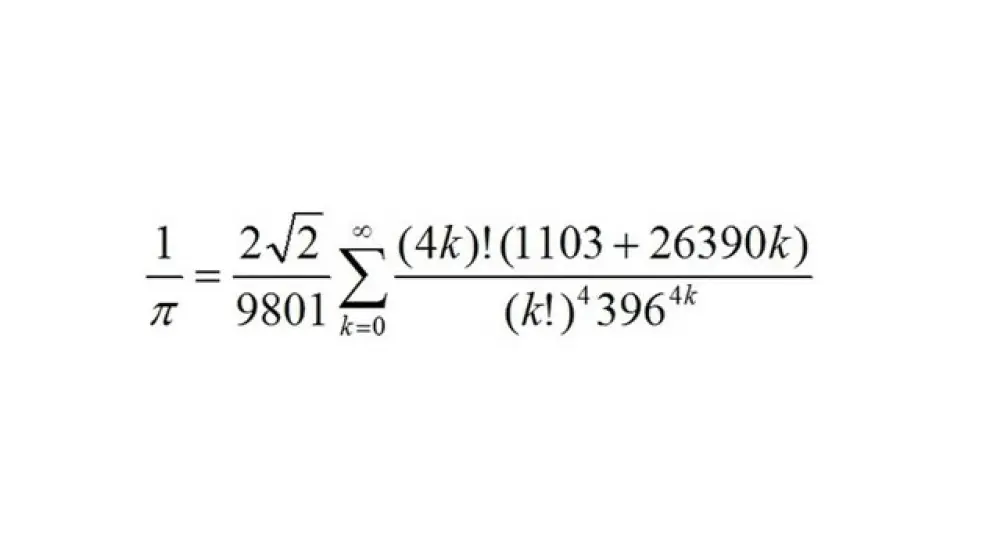
Recientemente el zaragozano Jesús Guillera obtuvo nuevas series de este tipo.

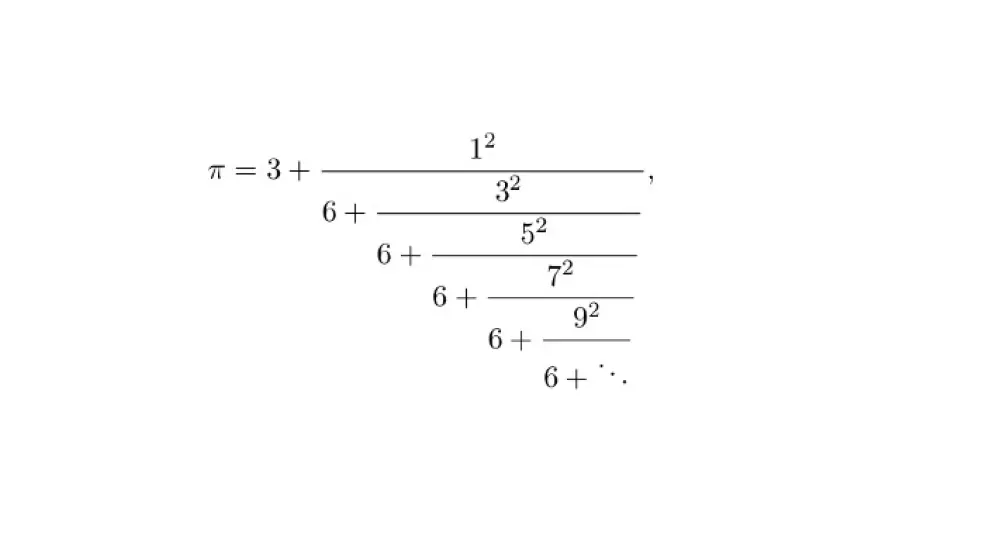
Otra forma de aproximar π es mediante fracciones continuas, como la siguiente de Lange (1999):

Entre tanto, también avanzaba el conocimiento teórico sobre π. En 1776, Lambert y Legendre demostraron su irracionalidad. En 1882, Carl von Lindemann demostró que π es un número trascendente (no existe polinomio de coeficientes enteros que lo tenga como raíz), lo cual implica que el antiguo problema de la cuadratura del círculo con regla y compás es imposible.

Tras la II Guerra Mundial, el uso de ordenadores cada vez más potentes permitió conocer un número cada vez mayor de cifras mediante algoritmos que usan las citadas series. En 1949, John Von Neumann con ENIAC, uno de los primeros ordenadores, trabajando 70 horas consigue 2.037 dígitos. En 1973 se llega al millón de dígitos. En 2010, a los 5 billones. Hoy se conocen más de 22,5 billones de cifras de π. Cualquier ordenador doméstico puede calcular un buen número de ellas. La app SuperPi evalúa la velocidad de proceso de las CPU mediante el cálculo de los primeros 4 millones.

Todos los libros en pi

Está muy aceptada la conjetura de que π es un número normal. Eso significa que en su parte decimal aparece cada uno de los 10 dígitos infinitas veces, distribuidos uniformemente, es decir, todos aparecen con la misma probabilidad y están todas las combinaciones posibles de ellos. Los más de 22 billones de cifras hasta hoy conocidas dan a entender que la conjetura es cierta, pero aún no ha sido demostrada de modo general. Sí que es normal con seguridad, por su propia construcción, el llamado ‘número de Champernowne’: 0,12345678910111213…

Esa propiedad es muy sugestiva. Supone, por ejemplo, que entre las cifras de π esté, codificado como número, cualquier libro. Pensemos en ‘El Quijote’. Su comienzo, "En un lugar de la Mancha…", si cada letra se expresa en el código ASCII, se convierte en la secuencia 069110032117110032108117103097114032100101032076097… Si π es normal, esa secuencia está en su parte decimal. Y también el libro entero. Y cualquier libro escrito en cualquier idioma. Y cualquier libro posible, aún no escrito.

A la espera de que la conjetura sea demostrada, comprobemos que nuestra fecha de cumpleaños está entre las cifras de π. Puedes consultarlo aquí. 

Demasiadas cosas que son casi pi

Son muy populares, demasiado, las supuestas explicaciones mágicas del mundo basadas en conspiraciones, seres desconocidos o claves secretas. Una de esas claves sería el número π. El propio Newton dijo que "la naturaleza se reduce a un número: pi. Quien descubra el misterio de pi, comprenderá el pensamiento de Dios...". Pero recordemos que, pese a su enorme genio científico, Sir Isaac dedicó buena parte de su tiempo al estudio de disciplinas tan poco científicas como la teología o la alquimia.

Se argumenta, por ejemplo, que la aceleración de la gravedad es casi π²; que un año terrestre dura casi π·10 elevado a 7 segundos; que el cociente entre la longitud de un río y la distancia entre sus extremos es casi π; etc. Esos ‘casi’ solo revelan la voluntad de encontrar π a toda costa. De la infinidad de datos observables, se escogen aquellos que, convenientemente operados, se acerquen a 3 y pico, despreciando todos los demás. Se llama apofenia a esa obsesión por detectar patrones predeterminados.

Mención especial merece el llamado misterio de la gran pirámide de Kheops, que ha dado lugar nada menos que a suponer su construcción por extraterrestres. El cociente entre el perímetro de la base y el doble de su altura resulta ser π. Tal cosa ocurrirá siempre que se midan las distancias con una rueda de radio unidad (algo usual ya en el Antiguo Egipto) y se tome como altura en unidades el mismo número elegido para el perímetro en vueltas de rueda. El ‘misterio’ de π en la pirámide no viene de otro planeta, está en la rueda.

José María Sorando matematicasentumundo.es

-Ir al suplemento Tercer Milenio

¿Te atreves a resolver un sudoku circular?