Comencemos contando una historia: 22 de febrero de 2020, para situarnos, unas tres semanas antes del confinamiento, ¡qué tiempos aquellos …! Ciudad de Bartow, estado de California. El acróbata Mike Hughes se monta en un cohete casero con el que pretende llegar a una altura de 1.500 metros. Su idea es la siguiente: si es capaz de llegar hasta esa altura y no percibe la curvatura de la Tierra, es porque la Tierra es plana.

Por desgracia, en el momento del despegue, el paracaídas se desprende del cohete, mientras que el cohete, con Mike dentro, sube, sube y sube durante 30 segundos que se hacen interminables. Sin paracaídas que frene el descenso, el experimento termina en tragedia.

Acabamos de asistir a una muerte por terraplanismo, efectivamente una muerte por terraplanismo.

Aunque pueda parecer mentira, este suceso ocurrió realmente, pero si tienes dudas de su veracidad, no tienes más que buscar Mike Hughes en internet y encontrarás muchas noticias de periódicos e informativos que se hacían eco del accidente.

En un contexto un poco más cercano, hace algo más de un mes, concretamente el 10 de septiembre, Barcelona acogió el Encuentro Tierra Plana, al que asistieron más de 500 personas. Según parece, en una época en la que tenemos más acceso a la información que nunca, da la impresión de que, a veces, nos alejamos del conocimiento.

Sin embargo, la intención de este artículo no es rebatir los argumentos del terraplanismo. Este debate quedó más que zanjado ya en el siglo IV a.C., cuando Aristóteles de Estagira estudió las consecuencias que tendría una Tierra esférica, corroborando que esta forma de la Tierra explicaba, con éxito, todos los fenómenos relacionados con la forma de nuestro planeta. El verdadero objetivo de estas líneas es presentar el experimento que llevó a cabo la primera persona que consiguió medir el tamaño de la esfera terrestre.

Te puede interesar

Muere el aventurero Mike Hughes tras lanzarse en un cohete casero para llegar al espacio y demostrar que la Tierra es plana

Así sería el mundo si la Tierra fuese plana

El protagonista de esta historia –como ocurre en muchas historias matemáticas– era griego, se llamaba Eratósthenes y vivió en Alejandría en el siglo III a.C. De él se podría decir que ‘tocó todos los palos’ del conocimiento, pues hizo contribuciones importantes en astronomía, matemáticas, geografía, filosofía e incluso poesía. Además, por si fuera poco, también fue director de la extraordinaria biblioteca de Alejandría.

Y al parecer, fue en dicha biblioteca donde encontró unos papiros con informes de observaciones realizadas en un puesto avanzado de Siena (actual Asuán), ciudad situada a unos 5.000 estadios al sur de Alejandría (aproximadamente 800 kilómetros). 

Según se indicaba en dichos informes, en el solsticio de verano (21 de junio), a mediodía, los objetos no arrojaban sombra en Siena. Tal curiosidad geométrica se puede describir como que en ese preciso instante los habitantes de Siena tenían el Sol exactamente sobre sus cabezas.

Este hecho podría pasar desapercibido para cualquier hijo de vecino, pero no para el curioso Eratósthenes, que decidió realizar la misma observación, pero en Alejandría. Así, a mediodía del solsticio de verano constató que en Alejandría, al contrario de lo que ocurría en Siena, los objetos sí arrojaban sombra, es decir, en ese instante, de ese día, los alejandrinos no tenían el Sol exactamente sobre sus cabezas, sino que lo veían con una cierta inclinación sobre la vertical. Además, fue capaz de medir el ángulo de esta inclinación, A, que era aproximadamente una cincuentava parte del ángulo completo, es decir unos 360º/50=7,2º (Figura 1).

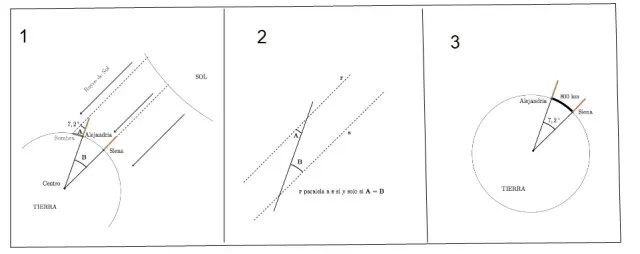
Como buen griego culto que era, Eratósthenes dominaba la geometría conocida en aquella época y sabía que el ángulo A y el ángulo B formado por el centro de la Tierra y las ciudades de Alejandría y Siena (Figura 1) son iguales, ya que son los alternos internos que resultan de cortar dos rectas paralelas con una tercera recta secante a ambas, (Figura 2).

Puesto que ambas ciudades están a unos 800 kilómetros de distancia y esto corresponde a una cincuentava parte de la circunferencia terrestre, Eratósthenes obtuvo que la longitud de la circunferencia terrestre era aproximadamente de unos 50 x 800 = 40.000 kilómetros (Figura 3).

Puesto que el radio (R) de una circunferencia y su perímetro (P) guardan la conocida relación P=2πR, la medición de Eratósthenes nos permite concluir que el radio de la Tierra es R= 40.000 km/2π, es decir, unos 6.366 km. ¡Eureka!

Atención a la genialidad de Eratósthenes que, hace más de 2.000 años, calculó –con una precisión muy aceptable– el tamaño de la esfera terrestre (cuyo radio es de unos 6.371 km) sin más que usar obeliscos, sombras, un poco de geometría y, sobre todo, muchísimo ingenio.

Víctor M. Manero profesor de la Universidad de Zaragoza y miembro de la comisión de divulgación de la Real Sociedad Matemática Española (@pitimanero)

-Ir al suplemento Tercer Milenio

Apúntate y recibe cada semana en tu correo la newsletter de ciencia