Ciencia de frontera: Fases de Berry y materiales del futuro

¿Qué tienen en común el mecanismo por el que un gato consigue caer siempre de pie, el aparcamiento en línea de un coche, el péndulo de Foucault (que seguramente habrás visto en algún museo de ciencias) y el método más preciso conocido para medir la resistencia eléctrica?

En todos estos ejemplos, un conjunto de parámetros del sistema ha realizado una evolución cíclica y, sin embargo, al volver al punto inicial, algo ha cambiado. En el caso de nuestro gato, este deforma su cuerpo durante la caída de forma que, aunque la forma es esencialmente la misma al principio y al final, su cuerpo ha rotado 180 grados. Esto es un efecto puramente geométrico: si el gato fuese rígido, la conservación del momento angular, principio básico de la mecánica clásica, le habría impedido hacerlo. De forma más profunda, todos los ejemplos se basan en una propiedad matemática conocida como fase geométrica (que es un ejemplo de lo que matemáticamente se conoce como holonomía).

Un sencillo ejercicio

Puedes hacer un sencillo ejercicio para convencerte de la existencia de estas fases geométricas: extiende el brazo derecho delante de ti con el pulgar hacia arriba; levanta el brazo rígidamente hasta tu cabeza; gira el brazo hacia la derecha hasta que esté perpendicular al cuerpo (el pulgar debería estar apuntando hacia atrás); gira el brazo de nuevo horizontalmente hasta la posición inicial de partida. Tu brazo está en la misma posición inicial pero el pulgar ahora está a 90 grados de la posición de partida apuntando hacia tu derecha. El brazo ha regresado a su posición inicial, pero el pulgar no, a pesar de que no has realizado ninguna rotación del brazo sobre su eje. Hemos producido un cambio global en la posición del pulgar sin ninguna rotación local del pulgar con respecto al brazo (técnicamente decimos que el brazo es un sistema no-holonómico).

Una relación desapercibida

Las holonomías son bien conocidas en matemáticas. Sorprendentemente, en 1984 el físico Michael Berry encontró una relación básica entre holonomía y muchos fenómenos de la mecánica cuántica que había pasado desapercibida.

La mecánica cuántica describe la materia en forma de ondas, con una fase que depende de cuánto se ha desplazado la onda y del tiempo que ha tardado en llegar a un punto. Lo que encontró Berry es que, además, la fase depende del circuito que la onda ha recorrido para llegar y de cómo ha cambiado la estructura interna de la onda. En su honor, esta contribución a la fase se conoce como fase de Berry.

Lejos de ser una curiosidad, desde el trabajo de Berry se han descubierto fases geométricas en casi todos los campos de la física: física del estado sólido, física de altas energías, óptica, mecánica de fluidos, gravedad y cosmología. En particular, la fase de Berry es un concepto especialmente importante en la física de la materia condensada, donde se manifiesta en diversos tipos de materiales y de propiedades.

La naturaleza topológica de la fase de Berry (que no depende de la forma exacta del ciclo realizado, sino de propiedades globales) se manifestó históricamente en el descubrimiento del efecto Hall cuántico. Cuando se crean materiales de manera que sus electrones se mueven en dos dimensiones, en presencia de altos campos magnéticos aparece una propiedad de la conducción eléctrica: la resistencia Hall. Al estudiarla desde el punto de vista cuántico, se vio que no depende ni de los materiales (que siempre tienen defectos) ni del tamaño del sistema. Es tal su importancia que se utiliza como patrón mundial de resistencia eléctrica.

Y lo que vino a continuación fue un ejemplo del formidable poder de la generalización en ciencia y de las ventajas de entender los fenómenos desde distintos puntos de vista: si bien el efecto Hall cuántico se entendía para el sistema concreto donde se descubrió, al estudiarlo desde la perspectiva de las fases de Berry se comprendió que, en realidad, formaba parte de una categoría más amplia de fenómenos físicos. Esto inició una línea de investigación muy fructífera en ciencia de materiales.

Así, hoy está sólidamente establecido que hay otros tipos de efectos Hall cuantizados que no solo afectan a la corriente eléctrica y que la topología y las fases de Berry juegan un factor fundamental en las propiedades de polarización eléctrica de sólidos y la conducción eléctrica en grafeno, y se ha descubierto un nuevo tipo de materiales, los llamados aislantes topológicos, que son aislantes en el volumen pero conducen por la superficie.

INMA-Colloquia

Sir Michael Berry es profesor emérito de Física en la Universidad de Bristol (Reino Unido). El jueves 20 de mayo a las 16.00 ofrecerá la charla ‘Geometric phases’, en la que resumirá la historia de su descubrimiento, los antecedentes y ramificaciones. El segundo de los coloquios organizados por el Instituto de Nanociencia y Materiales de Aragón (INMA, centro mixto CSIC-Unizar) podrá seguirse en directo por Zoom previa inscripción o el canal de Youtube del INMA.

Qué es la fase

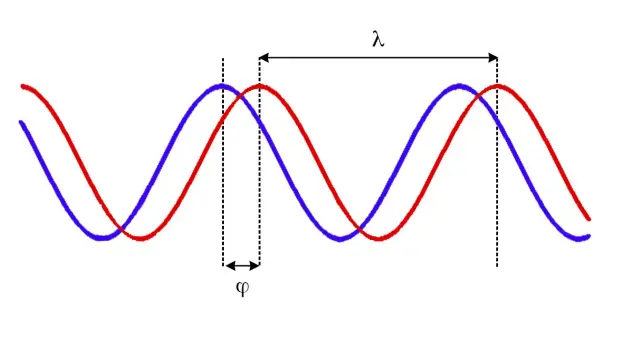
Dos ondas armónicas de igual amplitud y misma longitud de onda (lambda, distancia ente dos máximos o mínimos) pero desfasadas una distancia phi.

A lo largo de todo este artículo hablamos del concepto de fase de una onda, como puede ser el sonido que escuchamos o las ondas que observamos en un estanque si lanzamos una piedra. La fase determina el estado de vibración de un punto de la onda en un instante de tiempo determinado. Las diferencias de fase de dos ondas son muy relevantes, por ejemplo, al estudiar fenómenos de interferencia. Así, dos ondas iguales pero desfasadas en media longitud de onda se anulan la una a la otra; es lo que utilizan los auriculares con cancelación de ruido.

Espintrónica y nanofotónica

En el Instituto de Nanociencia y Materiales de Aragón, diversos grupos de investigadores trabajan en estos nuevos materiales topológicos desde hace años. De hecho, en los años noventa se desarrolló el patrón de resistencia español, basado en el efecto Hall cuántico, que utilizaba una bobina superconductora y un comparador criogénico de corriente basado en detectores SQUID.

En la actualidad, se trabaja en la versión que explota el espín del electrón, el llamado efecto Hall de espín. Asimismo, se estudian otras formas de controlar la propagación del espín gracias a la creación de fases de Berry mediante la estructuración de los materiales en la nanoescala, dentro del campo de la espintrónica y espín-caloritrónica. Dado que sería eficiente sustituir las corrientes eléctricas por las de espín, estos estudios tienen gran interés en tecnologías de la información y electrónica de bajo consumo.

También se trabaja en nuevos fenómenos en nanofotónica, donde se están diseñando nanoestructuras que, mediante la fase de Berry, impartan una rotación a la luz, con la idea de poder detectar pequeñas cantidades de moléculas biológicas quirales.

Luis Morellón Alquézar y Luis Martín Moreno Investigadores del Instituto de Nanociencia y Materiales de Aragón (CSIC-UZ)

-Ir al suplemento Tercer Milenio

Apúntate y recibe cada semana en tu correo la newsletter de Tercer Milenio