Tercer Milenio
En colaboración con ITA
Estimador de probabilidad
Qué riesgo tienes de coincidir con un positivo en covid-19 si asistes a un evento
Una plataforma desarrollada en el BIFI estima el riesgo en función de la incidencia.
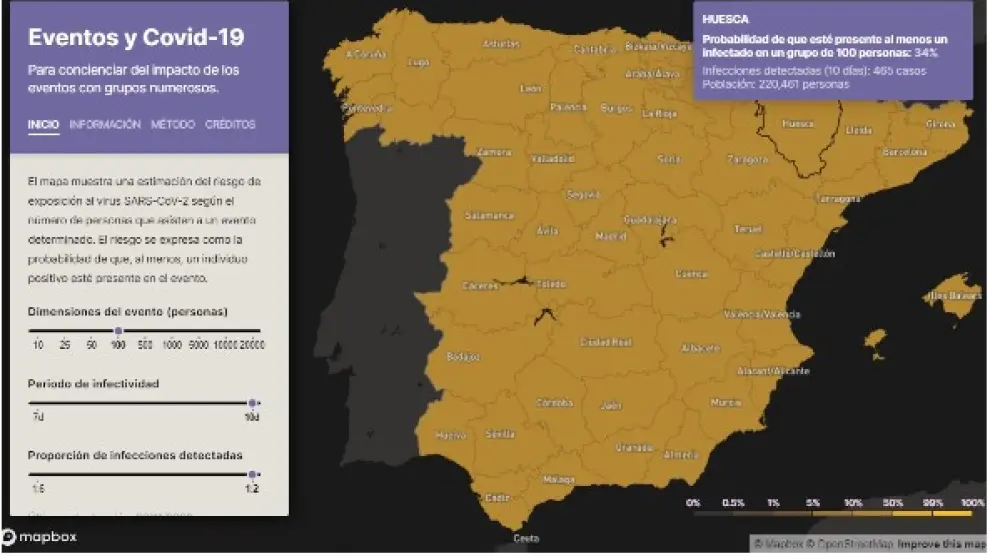
Diversas restricciones limitan nuestros movimientos y nuestra vida social para frenar la transmisión de la covid-19. Como nos cuesta tanto evaluar riesgos, una estimación concreta puede dejarnos ver muy claramente por qué no hay que hacer encuentros que reúnan a mucha gente. Por ejemplo, en la provincia de Huesca, la probabilidad ahora mismo de que al menos una persona estuviera infectada en una boda de 100 invitados sería del 34%.
Así lo estima la plataforma desarrollada por investigadores del Instituto de Biocomputación y Física de Sistemas Complejos (BIFI) de la Universidad de Zaragoza para concienciar del impacto de los eventos con grupos numerosos. El mapa muestra, por provincias, "una estimación del riesgo de exposición al SARS-CoV-2 según el número de personas que asisten a un evento –explica Yamir Moreno, investigador del BIFI–. El riesgo se expresa como la probabilidad de que al menos un individuo positivo esté presente en él". El usuario puede interactuar y ver cómo aumenta ese riesgo al crecer el tamaño del evento (en la misma provincia, a partir de 500 personas la probabilidad de coincidir con al menos un positivo es del 88%). El mapa se actualiza diariamente con los datos oficiales de incidencia de la covid-19.
Los investigadores advierten que esta herramienta no expresa el riesgo de contraer la enfermedad, que depende también de factores como la duración del evento, el espacio en que se desarrolla y las medidas de protección.
Loterías y apuestas
Los humanos no somos precisamente buenos para evaluar el riesgo al que nos enfrentamos en cada ocasión. "Por ejemplo, tendemos a ponernos en la minoría cuando se trata de algo que no nos favorece, como cuando tenemos miedo a subirnos a un avión y no en un coche, a pesar de que la probabilidad de tener un accidente mortal en coche es 86 veces superior a tenerlo si viajamos en avión –explica Moreno–. Por el contrario, si es algo positivo, como ganar en la lotería, no nos importa arriesgar o, en este caso, invertir".
Durante la pandemia, muchos se hacen una pregunta similar a las anteriores: ¿cuál es la probabilidad de que me contagie de covid-19 si asisto a un evento de un determinado tamaño? "Esta pregunta no tiene una respuesta universal y depende de factores como la susceptibilidad que tenemos cada uno de nosotros a contraer o transmitir el virus", precisa. "Lo que sí podemos aproximar es cuál es la probabilidad de que una persona que asista a ese evento o reunión sea positiva para el SARS-CoV-2".
Moreno explica que, para responder a esta pregunta "es más sencillo estimar la probabilidad de justo lo contrario. Por ejemplo, si vamos al estadio a ver un partido de fútbol, ¿cuál es la probabilidad de que ninguno de los 50.000 espectadores esté infectado? Consideremos ahora a cada uno de los espectadores. Si de los aproximadamente 47 millones de personas en España 1.000 están infectadas, la probabilidad de no estar infectado se puede estimar en 46.999.000/47.000.000, o sea, una probabilidad del 99,9978%. Una óptima perspectiva desde un punto de vista individual. En términos de apuestas, estamos hablando de un suceso favorable ¡47.000 a 1!". Ahora bien, prosigue, "¿cuál es la probabilidad de que todas, las 50.000 personas, no sean positivas? Desde un punto de vista de cálculo probabilístico, esto es equiparable a ganar 50.000 apuestas simultáneamente. Aunque cada apuesta tiene una probabilidad muy alta de ganar, no es fácil ganarlas todas. Esta probabilidad se puede calcular multiplicando la de una sola victoria (0,999978...) por sí misma 50.000 veces. Entonces obtendremos que la probabilidad de ganar todas las apuestas es solo del 34,5%. En otras palabras, la probabilidad de que al menos un espectador resulte positivo para el SARS-CoV-2 es del ¡65,5%!"
La web ‘Eventos y covid-19’ es parte de un proyecto internacional en el que colaboran investigadores estadounidenses del Instituto de Tecnología de Georgia y la Northeastern University y de la Fundación ISI de Turín (Italia). Primero se hizo para Estados Unidos y ahora ya está implementado en Italia y Reino Unido. España es el cuarto país que se añade y el Grupo de Redes y Sistemas Complejos (Cosnet) del BIFI es el responsable del proyecto. "La idea es extender el análisis a cuantos más países mejor".
Qué evalúa
El riesgo de encontrar a una persona afectada por la covid-19 en una provincia específica depende de tres factores:
- Casos La estimación de la prevalencia de casos en la provincia viene dada por el número de casos detectados por el sistema de vigilancia en un intervalo comprendido entre los 7 y 10 días anteriores.
- Detectados Hay casos que escapan al sistema de vigilancia. El factor de subestimación de infecciones, es decir, cuántos somos capaces de detectar en relación al número de casos reales, puede variar entre 1:2 (1 de cada 2 infectados reales) y 1:6 (1 de cada 6 infectados reales) e introduce un factor correctivo para estimar la prevalencia real del número de infectados.
- Tamaño Número de participantes en el evento.
Una Zaragoza sintética para simular el efecto de las restricciones
¿Cuánto bajaría la transmisión si confinamos perimetralmente Zaragoza y se decreta también el toque de queda? Y si además cerramos los bares, ¿cuál sería la diferencia? Los modelos computacionales predicen, permiten ‘probar con gaseosa’ cualquier medida. Simular su efecto y ver qué pasaría, con la principal función de ayudar a la toma de decisiones. Pero para eso hay que meter la ciudad en el ordenador. El grupo de Yamir Moreno en el BIFI va a "adaptar los estudios que hemos venido haciendo en EE. UU. a Aragón y a España después". Empezarán por crear una Zaragoza sintética, incorporando datos de censo, edad, demografía, distribución de centros de trabajo y escuelas, etc. Así, "tendremos una población estadísticamente equivalente a la real". Luego, habrá que generar las interacciones entre individuos y finalmente aplicar el modelo epidemiológico. En el caso de Boston, disponían de datos de telefonía móvil, "como aquí no tenemos ese tipo de información, generaremos las interacciones y las redes de contacto de manera artificial, pero informados por datos y modelos de movilidad". Sabe que "no será tan preciso como el de Boston, pero creemos que el resultado promedio de muchas realizaciones de sociedades artificiales y evolución de la epidemia será bastante fiable". Estos modelos "no te dicen lo que tienes que hacer, pero son una herramienta que permite anticiparse".
-Ir al suplemento Tercer Milenio
Apúntate y recibe cada semana en tu correo la newsletter de Tercer Milenio
![A pedestrian walks across an empty street amid the coronavirus disease (COVID-19) outbreak in Boston, Massachusetts, U.S., May 18, 2020. REUTERS/Brian Snyder [[[REUTERS VOCENTO]]] [[[HA ARCHIVO]]] HEALTH-CORONAVIRUS/USA](https://imagenes.heraldo.es/files/image_320_180/uploads/imagenes/2020/06/12/outbreak-of-the-corona-34810618.jpeg)