Tercer Milenio
En colaboración con ITA
Matemáticas contigo
Sandías, besos y guerra
Tal vez la sandía sea la fruta más veraniega. Aparte de pepitas, también entre sus carnes se encuentran matemáticas.

Recuerdo los veranos en la casa de mis abuelos maternos en San Juan de Mozarrifar. Las barquillas llenas de manzanas, patatas, melones y sandías se apilaban en el corral antes de guardarlas en el antiguo granero. De todas las frutas, el sabor de la sandía, para mí, será el sabor del verano.
Almacenar sandías en barquillas no resultaba muy ventajoso. A veces con dos sandías, se llenaba la caja, dejando alrededor gran cantidad de espacio libre. En cierta forma, la forma esférica de las sandías no encaja bien con la ortogonalidad de las cajas. Abstrayendo y simplificando el problema, podemos pensar que las sandías son esferas todas de igual radio r.
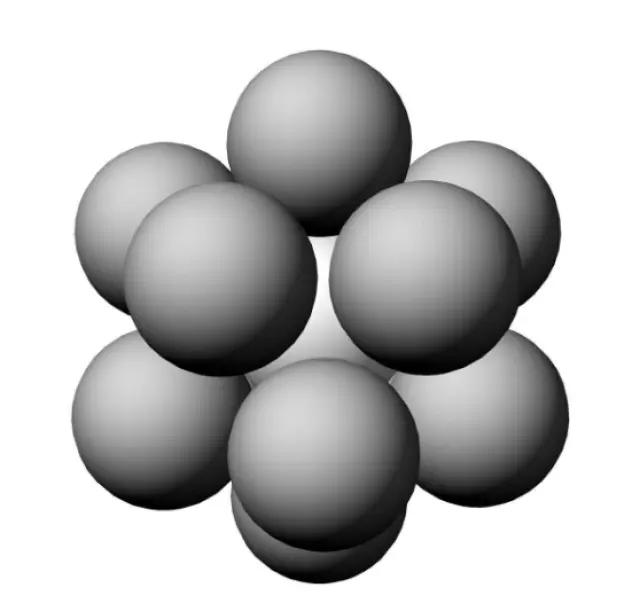
Un primer problema es calcular cuántas sandias (esferas) se pueden colocar alrededor de una central tocando (besando) todas ellas a la central. Este número se conoce como el número de besos. En dimensión 1, las esferas son intervalos y el número de besos igual a 2. En dimensión 2, las esferas son círculos y con monedas o galletas, es fácil comprobar que el número de besos es igual a 6. En cambio, en dimensión 3, las cosas se complican.
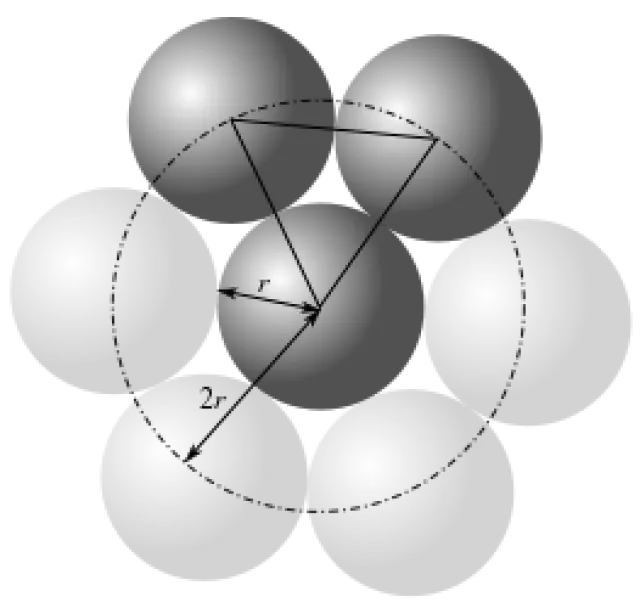
Vamos a hacer un pequeño cálculo que aclara el resultado. Tomemos una esfera de radio r, y calculemos cuántas medias esferas podemos poner colocar alrededor de esta esfera inicial. Consideramos medias esferas (y no enteras), ya que así minimizamos el espacio que no podemos rellenar. La esfera central y las medias esferas están incluidas en una esfera exterior de radio 2r.
Obtengamos el espacio que hay para medias esferas V= 4/3π(2r)³-- 4/3πr³-= 28/3 π r³. Si dividimos por el volumen de media esfera 2/3πr³, habría espacio para 14 esferas justas. Pero está claro que, al colocar dos esferas juntas, se pierde espacio. Entonces podrán ser 13, o incluso menos 12, dependiendo de la cantidad de espacio que se pierda.
A finales del siglo XVII, David Gregory, matemático y admirador de la obra de Sir Isaac Newton, lo visitó en la Universidad de Cambridge. Durante días trataron numerosos temas científicos, filosóficos e incluso religiosos. Gregory hacía anotaciones en un cuaderno. En una discusión de astronomía, se plantearon las posibles distribuciones de estrellas orbitando alrededor de un sol central. Inmediatamente surgió el problema de los besos en dimensión 3, ¿cuántas esferas pueden estar en contacto con una esfera central sin superponerse? Gregory apostaba que eran 13, mientras que Newton, 12, ambos apoyándose en argumentos matemáticos. En 1950 se recuperó este problema del propio cuaderno de Gregory y, tres años más tarde, se demostró que Newton tenía razón, como casi siempre. Así que, si tenemos sandías perfectamente esféricas y de igual radio, solo podremos poner 12 alrededor de una sandía central.
Pero esto no resuelve el problema del empaquetamiento. Mi abuelo Perico ha tenido una cosecha extraordinaria. Quiere apilar sus sandías (esferas) en un espacio infinito dejando libre la menor cantidad de espacio posible, y así conseguir la densidad de empaquetamiento más alta. Este problema se conoce en matemáticas como la conjetura de Kepler.
El origen del problema surge en el puerto inglés de Plymouth en 1585, a bordo del navío inglés 'El tigre'. Sir Walter Raleigh, pirata y hombre de confianza de la reina Isabel I, comanda una expedición para crear una colonia en Virginia. El matemático y astrónomo Thomas Harriot acompaña a Raleigh y le surge de forma natural el problema de apilar las balas de cañón (esferas) ocupando el menor espacio posible en el navío. Harriot trabajó el problema y en 1606 escribió a su amigo Johannes Keppler, quien se interesó por el problema.
En 1611, como regalo de cumpleaños a Su Majestad, Rodolfo II, y en respuesta a las acusaciones de inutilidad de su cargo, Kepler le dedicó al emperador el ensayo 'El copo de nieve de seis esquinas'. En este librito, que muchos consideran el fundamento de la cristalografía, Kepler expone la formación de los copos de nieve. También menciona la cuestión planteada por Harriot. A pesar de no dar una demostración rigurosa, Kepler afirma que “al igual que los fruteros colocan sus frutas (aludiendo al ejemplo concreto de las naranjas), la sabiduría centenaria indicaba que el sistema más adecuado era el del apilamiento en forma de pirámide”. Esta solución para el empaquetamiento óptimo de esferas, ¿se podría demostrar matemáticamente?
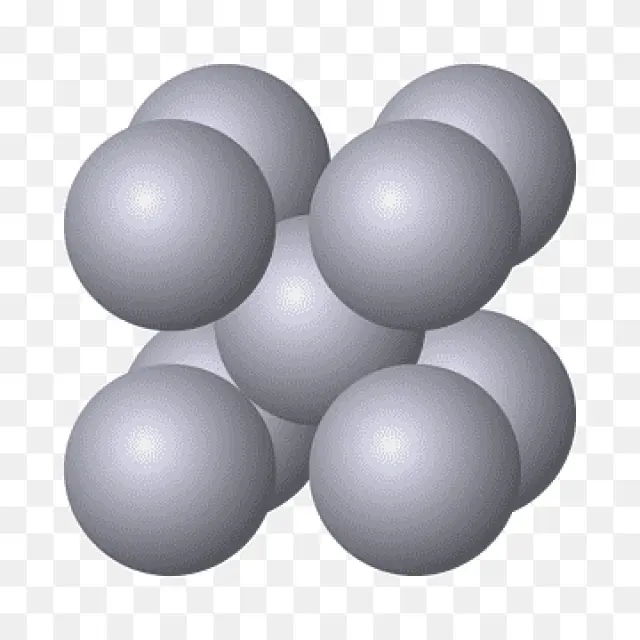
En dos dimensiones, la disposición hexagonal, en forma de panal, que hemos comentado con monedas o galletas es la que consigue mayor densidad (con una densidad del 91% aproximadamente). El problema de las esferas tridimensionales resultó ser más difícil aún. Hubo que esperar hasta 1998 para que el matemático estadounidense Thomas C. Hales (asistido con ordenador) demostrase que el empaquetamiento de esferas en pirámide era óptimo, siendo su densidad aproximada del 74 %.
Pero la matemática no se detiene. Se puede seguir, considerar esferas en espacios de dimensión arbitraria y buscar el empaquetamiento óptimo en estos espacios. Si en dimensión 3 el problema es de extrema dificultad, al aumentar la dimensión la complejidad estalla. En 2016 la matemática ucraniana Maryna Viazovska de 31 años encontró en los espacios de dimensión 8 y 24 los empaquetamientos óptimos. Las densidades de estos empaquetamientos son del 25% y del 0,2% respectivamente. Las densidades decrecen rápidamente al aumentar la dimensión.
Los logros de Viazovka la han llevado a ganar la Medalla Fields, el máximo reconocimiento de la comunidad matemática internacional en este año 2022. Es la segunda mujer en obtener tal galardón y, en el acto de entrega, le dedicó el premio a Yulia Zdanovska, matemática de 21 años asesinada en un ataque ruso con misiles en la ciudad de Járkov, al inicio de la guerra.
La terrible guerra de destrucción masiva que vive Ucrania ha movilizado a la comunidad internacional, y también a los matemáticos. El Congreso Internacional de Matemáticos (conocido como ICM por sus iniciales en inglés) que se iba a celebrar en la ciudad rusa de San Petersburgo en julio de 2022 se trasladó a Helsinki, expulsando a la delegación rusa. Por su parte, en una carta abierta firmada por cerca de 7.000 científicos y académicos rusos en marzo de 2022 y dirigida al presidente Vladimir Putin, protestaban "enérgicamente" contra la guerra en Ucrania, afirmando que "ningún interés geopolítico puede justificar los muertos y el baño de sangre. La guerra solo llevará a la pérdida total de nuestro país, para el que trabajamos".
Recuerdo a mi abuelo Perico regresando del huerto en su bicicleta. Era capaz de empaquetar frutas y hortalizas perfectamente en su barquilla, desconociendo la alta matemática. Se sorprendería con las sandías cúbicas o con las de forma de corazón que hoy se producen. Pero sabía que, en su interior, las sandías, como las personas, escondían maravillosos secretos.
Pedro J. Miana Departamento de Matemáticas, IUMA & Facultad de Ciencias, Universidad de Zaragoza
-Ir al suplemento Tercer Milenio
Apúntate y recibe cada semana en tu correo la newsletter de ciencia



