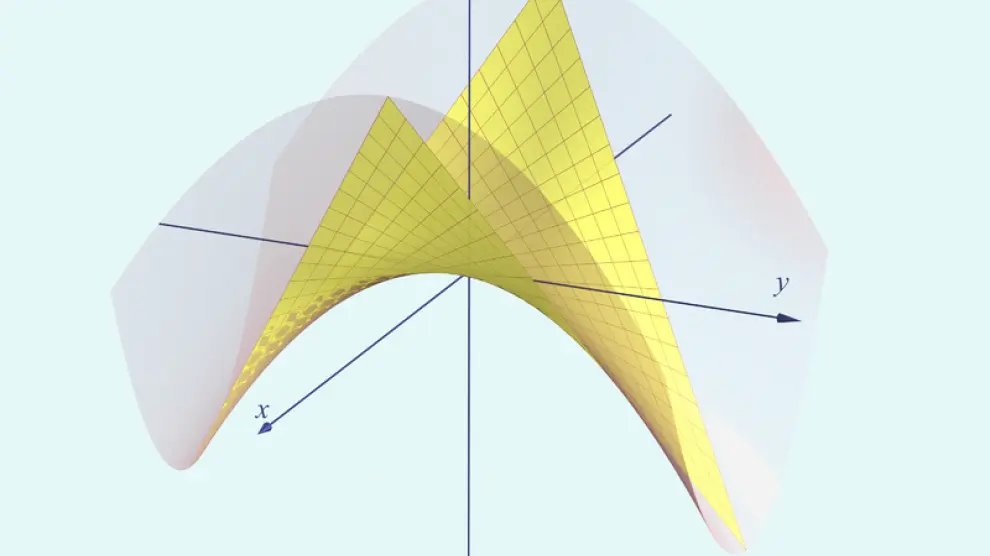
Modulación El módulo básico es de 15 metros y el ‘número secreto’ del templo es el 12. De los divisores del doce surge el sistema de proporciones en la Sagrada Familia (1, 1/3, 1/4, 1/2, 3/4, 2/3, 1). Movimientos helicoidales y helicoides Este principio combina de forma compleja rotaciones en torno a un eje y traslaciones en la dirección del eje, creando un interesante movimiento vertical ligado a las hélices cilíndricas, el helicoide y las rampas helicoidales. Muchas columnas, escaleras de caracol, etc., muestran este principio. Intersección de formas La operación, compleja, de intersecar diversas figuras geométricas culmina en la Sagrada Familia con las superficies regladas, elipsoides y, muy especialmente, con la creación de los pináculos de las torres de los Apóstoles. Fractalidad El principio natural de la fractalidad en el crecimiento de las ramas de los árboles es aprovechado por Gaudí en el diseño de las columnas de la Sagrada Familia: el ‘tronco’ da paso por medio de los ‘nudos’ elipsoidales a nuevas columnas-ramas. El resultado:_una forma magistral de distribuir y transmitir las cargas. Polígonos Los polígonos planos regulares más usuales son los triángulos, cuadrados, pentágonos, hexágonos, octágonos, decágonos y dodecágonos. Las columnas de la Sagrada Familia nacen de un juego geométrico finísimo, moviendo polígonos e intersecando volúmenes. Poliedros En cuanto a poliedros, encontramos cubos, octaedros, dodecaedros o sus intersecciones, icosaedros y algún poliedro estrellado. Algunos de los poliedros más espectaculares aparecerán en los pináculos que aún deben construirse. Cónicas Circunferencias, elipses, parábolas e hipérbolas son curvas omnipresentes en muchas formas gaudinianas por ser secciones principales de las superficies regladas, piezas clave del repertorio geométrico. Hiperboloides de una hoja Estas notables superficies están formadas por rectas que se apoyan entre dos circunferencias iguales, paralelas y giradas, uniendo una colección bien definida de puntos correspondientes entre las dos curvas. Resulta también del giro de una hipérbola en torno al eje de simetría que no corta la curva. Fue una superficie introducida por Gaudí en arquitectura después de descubrir que era una forma óptima para campanas. Forman bóvedas, muchos soportes o entradas de luz en la nave de la Sagrada Familia. Paraboloides hiperbólicos El paraboloide hiperbólico, una de las superficies más importantes y originales usadas por Gaudí, es una superficie formada por rectas que se apoyan pautadamente en dos rectas que se cruzan en el espacio de forma ordenada. Si las dos rectas de apoyo fuesen paralelas, surgiría un plano, pero, al inclinarlas, surge esta superficie que tanto enamoró a Gaudí. En la actualidad, los paraboloides hiperbólicos tienen su culminación en los ventanales laterales del templo de la Sagrada Familia: los paraboloides hiperbólicos se acoplan a las sofisticadas formas de los hiperboloides de una hoja formando parte del ventanal. Pero la culminación absoluta en el uso de los paraboloides hiperbólicos se dará en la cubierta superior de las naves y sacristías, así como también en los campanarios y en las torres.